Le dépôt
pensée magique en mathématiques
mai 2017
L’objectif d’aujourd’hui est de prouver que la pensée magique est omniprésente en mathématiques. Tout d’abord, définissons la pensée magique. Je dirais que la pensée magique est une sorte de pensée métaphorique, comme dans la métaphore « Mon cœur est le soleil » seulement avec l'idée supplémentaire qu'écrire ces mots/créer la métaphore s'efforce de rendre la métaphore vraie dans une certaine mesure ou dans un certain sens. . La pensée magique est l’affirmation selon laquelle dire « Mon cœur est le soleil » réchauffe réellement mon cœur.
Maintenant, la manière dont les mathématiques utilisent la pensée magique consiste à commencer par une idée métaphorique de la différence. Par exemple, la différence entre un « corbeau » (1) et un « bureau » (2) métaphoriquement (pas réellement) est la différence entre le « l’étoile du nord » (3) et la « forme de pensée appelée questionnement » (4). Il est assez intuitif que la différence entre (1) et (2) est différente de la différence entre (3) et (4), mais les mathématiques fusionnent toutes les différences en un seul concept avec métaphore. Et c'est un type particulier de métaphore qui affirme que la différence en réalité fonctionne de cette façon.
Même si 3 et 5 sont moins différents (2) que 3 et 9, (6), ces différences ne sont pas prises en compte dans le symbole mathématique traditionnel de la différence, le  . Traditionnellement, 3
. Traditionnellement, 3  5 tout autant que 3
5 tout autant que 3  9, donc l'identité de la différence,
9, donc l'identité de la différence, 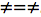 , est renforcée.
, est renforcée.
Les mathématiques affirment un concept ultime de « différence » qui est universel : elles fonctionnent pour toute situation où il existe une différence, rendant toute différence « complète », et elles le font en joignant métaphoriquement des différences disparates. Par conséquent, cela relève de ma définition de la pensée magique.
Je fais le contraire de ce que Derrida a fait avec sa Différance. Derrida a ajouté des sens à la différence lui permettant d'avoir une histoire et d'appartenir au langage, je propose que nous soustrayons, ou mieux divisions complètement la différence en différences.
Le reste des sciences emboîtant le pas, bien entendu, puisque les mathématiques sont le langage des sciences. Mon conseiller pour mon MS. en mathématiques a dit un jour : « les mathématiques sont la poésie des sciences ». Une poésie qui utilise encore et encore la métaphore de la Différence.
Andrew Nightingale
trad G&J